Merge Sort Example in C++

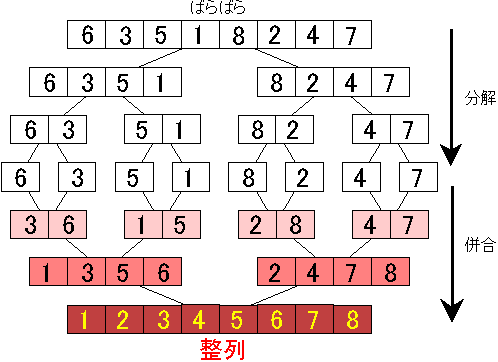
A merge sort is a O(n log n) sorting algorithm. I show in this example how to implement a merge sort in c++ using recursion. This algorithm is a divide & conquer based algorithm.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89

/*****************************************************************************
* Merge Sort has O(nlogn) compute time. Splits the list into two sublists then
* merges them back together sorting them
*****************************************************************************/
void mergeSort(list<int> &myList)
{
list<int> listOne;
list<int> listTwo;

bool sorted = false;
while (!sorted)
{
split(myList, listOne, listTwo);
if (listTwo.size() == 0)
sorted = true;
merge(myList, listOne, listTwo);
}
return;
}

/*****************************************************************************
* Splits a list into 2 lists
*****************************************************************************/
void split(list<int> &myList, list<int> &listOne, list<int> &listTwo)
{

listOne.resize(0);
listTwo.resize(0);

//While not at end of list
list<int>::iterator it = myList.begin();
while (it != myList.end())
{
int lastItem = 0;
while (it != myList.end() && *it >= lastItem)
{
listOne.push_back(*it);
lastItem = *it;
it++;
}

lastItem = 0;
while (it != myList.end() && *it >= lastItem)
{
listTwo.push_back(*it);
lastItem = *it;
it++;
}
}
return;
}

/*****************************************************************************
* Merges 2 lists taking the smaller number each time from both lists. Then
* copies the remaining numbers over if there are any left
*****************************************************************************/
void merge(list<int> &merged, list<int> &listOne, list<int> &listTwo)
{
merged.resize(0);
list<int>::iterator itOne = listOne.begin();
list<int>::iterator itTwo = listTwo.begin();
while (itOne != listOne.end() || itTwo != listTwo.end())
{
if (*itOne < *itTwo)
{
merged.push_back(*itOne);
itOne++;
}
else
{
merged.push_back(*itTwo);
itTwo++;
}
}
//Reached end of list One
if (itOne == listOne.end())
while (itTwo != listTwo.end())
{
merged.push_back(*itTwo);
itTwo++;
}
else //Reached end of list Two
while (itOne != listOne.end())
{
merged.push_back(*itOne);
itOne++;
}
return;
}

Merge Sort Algorithm:

Divide the unsorted list into n sublists until each list contains 1 element. If the list has 1 element it is sorted!
Repeatedly merge the sublists to produce new sublists until there is only 1 sublist remaining. The final list will be sorted!

Leave a Reply Cancel reply