Sudoku is one of my favorite games and I really enjoyed writing a sudoku solver. This sudoku procedural program was written in the language c++. The sudoku program allows you to input a board via a text file and allows you to save your progress. If you get stuck, the program can finish the board. I also spent the time to implement a colored board into the program. If you don’t understand the rules of sudoku or how to play sudoku then you can go here.
The ‘board’ is stored in an integer array called board[81]. I also have a Boolean array called isFixedValue[81] that keeps track of which numbers can or can’t be modified. This is decided when the board is opened. In order to make this algorithm easier I decided to also have a multidimensional Boolean array called isPossibleValue[81][9] that keeps track of each possible number for each square. For example, since 1,2,4,6,7, and 9 are not possible numbers for square #. Then isPossibleValue[4][1], isPossibleValue[4][2], isPossibleValue[4][4], isPossibleValue[4][6], isPossibleValue[4][7], and isPossibleValue[4][9] would all evaluate to false.
9 0 0|1 # 4|0 0 2
0 8 0|0 6 0|0 7 0
0 0 0|0 0 0|0 0 0
———————-
4 0 0|0 0 0|0 0 1
0 7 0|0 0 0|0 3 0
3 0 0|0 0 0|0 0 7
———————-
0 0 0|0 0 0|0 0 0
0 3 0|0 7 0|0 8 0
1 0 0|2 0 9|0 0 4
This allows my solve function to use human knowledge to solve the board. Obviously if the number 2 evaluates true in only one square on a single row then you can fill that number in. Likewise you can repeat for each column and block. The only downside to this is after going through all the rows and filling in some numbers you have to update your isPossibleValues[81][9]. That is what my checkPossibles(Board) function does. To allow some efficiency my checkPossibles will also fill in any numbers where there is only one possible value there. It can get complicated which is why I recommend writing a good algorithm. Since my board is colored it’s display function will only run on a windows machine and not linux. However this could easily be modified to run colored in linux. Below is just the solve function of my program. If you would like the full source it is posted at the bottom of this post. Remember to give credit where due.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 | /********************************************************************** * This will use human logic to attempt to solve a board * It will add the total number of possibles for each number * in each ROW, COLUMN, and BLOCK... * If the total is one it will fill that number in and update the possibles * in each square with the function checkPossibles ***********************************************************************/ float solve(Board &newBoard) { int coordinates = 0; bool noChanges; int startTime = clock(); do { noChanges = true; //Fill in one possible answer squares and exit if solved //We will do this after each Row, Column, and Block check if (checkPossibles(newBoard)) return true; //Fill in the known numbers for each ROW for (int i = 0; i < 81; i += 9) for(int guess = 1; guess <= 9; guess++)//Numbers 1 to 9 { int total = 0; //Test the number on the row for(int iRow = i; iRow < (i + 9); iRow++) if(!newBoard.isFixedValue[iRow]) total += newBoard.isPossibleValue[iRow][guess - 1]; if (total == 1)//We have found an answer! for(int iRow = i; iRow < (i + 9); iRow++) if (newBoard.isPossibleValue[iRow][guess - 1] && !newBoard.isFixedValue[iRow]) { newBoard.values[iRow] = guess; newBoard.isFixedValue[iRow] = true; noChanges = false; } } //Fill in one possible answer squares and exit if solved if (checkPossibles(newBoard)) return true; //This will fill in the known numbers for each COLUMN for (int i = 0; i < 9; i++) for(int guess = 1; guess <= 9; guess++)//Numbers 1 to 9 { int total = 0; //Test the number on the column for(int iColumn = i; iColumn < 81; iColumn += 9) if(!newBoard.isFixedValue[iColumn]) total += newBoard.isPossibleValue[iColumn][guess - 1]; if (total == 1)//We have found an answer! for(int iColumn = i; iColumn < 81; iColumn += 9) if (newBoard.isPossibleValue[iColumn][guess - 1] && !newBoard.isFixedValue[iColumn]) { newBoard.values[iColumn] = guess; newBoard.isFixedValue[iColumn] = true; noChanges = false; } } //Fill in one possible answer squares and exit if solved if (checkPossibles(newBoard)) return true; //This will fill in the known numbers for each BLOCK for (int r = 0; r < 81; r += 27) for (int c = 0; c < 9; c += 3) { int i = r + c;//Puts me at the beginning of each block for(int guess = 1; guess <= 9; guess++)//Numbers 1 to 9 { int total = 0; //Test the number on the column for(int iBlockR = i; iBlockR < (i + 27); iBlockR += 9) for (int iBlockC = iBlockR; iBlockC < (iBlockR + 3); iBlockC++) if(!newBoard.isFixedValue[iBlockC]) total += newBoard.isPossibleValue[iBlockC][guess - 1]; if (total == 1)//We have found an answer! for(int iBlockR = i; iBlockR < (i + 27); iBlockR += 9) for (int iBlockC = iBlockR; iBlockC < (iBlockR + 3); iBlockC++) if (newBoard.isPossibleValue[iBlockC][guess - 1] && !newBoard.isFixedValue[iBlockC]) { newBoard.values[iBlockC] = guess; newBoard.isFixedValue[iBlockC] = true; noChanges = false; } } } //Fill in one possible answer squares and exit if solved if (checkPossibles(newBoard)) return true; }while(noChanges == false); //If not solved by now, Time to use the big guns if (!isSolved(newBoard)) bruteForce(newBoard); //Output time it took to solve board return (clock() - startTime) / 1000.0; } |
See the full source code here: sudoku

January 16, 2010
I need the output for this program can i get that
March 6, 2010
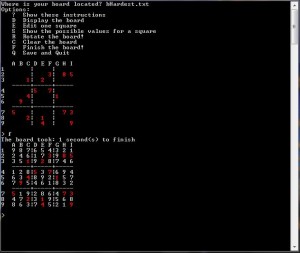
I included a screenshot of what the program output looks like.
March 22, 2010
..pls give me examples of your board
March 28, 2010
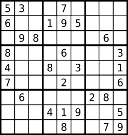
The boards are just stored as 9 rows by 9 columns of integers 0 to 9. I’ve included some random difficulty boards at the bottom of the post.