Month: March 2010

March 28, 2010 Software Development 5 Comments

RSA Encryption Explained Simply

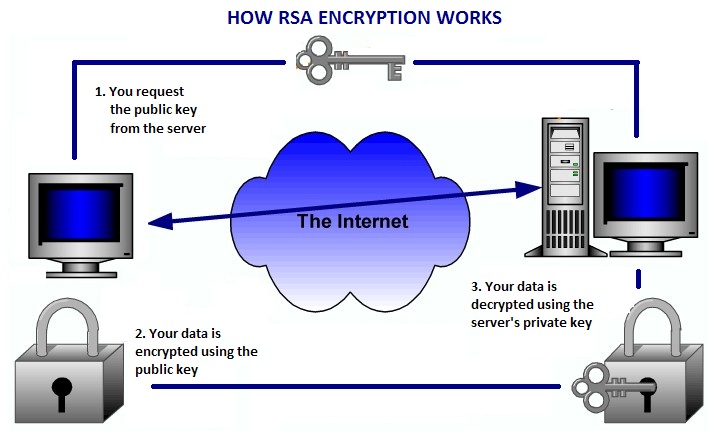
How RSA Encryption Works

RSA encryption is an Algorithm understood by so few people and used by many. In hopes to help that large percentage understand RSA Encryption better I wrote this explanation. If you ever visit a https site chances are you are using RSA encryption to encrypt or scramble the data sent over the internet. Since you could be sending important information like a credit card number it is imperative that you encrypt the data. The important thing is that we want to do this encryption process without requiring secret keys that both the sender and the recipient must posses. That’s where a system that uses a “Public Key” comes in handy.

Continue reading
March 7, 2010 Software Development Post a Comment

Extended Euclidean Algorithm in C++

Writing an Extended Euclidean Calculator that calculates the inverse of a modulus can get pretty difficult. However writing a good algorithm and going through step by step can make the process so much easier.  So we want to find a’ or inverse of a so that a * a’ [=] 1 (mod b). In other words we are trying to find an integer (a’) when multiplied by     a    and then divided by   b   gives you a remainder of   1. In order to find this number(a’), we have to work the Euclidean Algorithm backwards which is referred to as the Extended Euclidean Algorithm.

Continue reading
March 6, 2010 Software Development 4 Comments

Modular Exponentiation in C++

Modular Exponentiation is way of calculating the remainder when dividing an integer b (Base) by another integer m (Modulus) raised to the power e(Exponent). Fast modular exponentiation of large numbers is used all the time in RSA to encrypt/decrypt private information over the internet. Whenever you go to a secure site you are using RSA which deals with modular exponentiation.So lets understand modular exponentiation with c++!

Continue reading
March 6, 2010 Software Development 3 Comments

Fibonacci Calculator C++

Fibonacci sequence using Linked Lists

The fibonacci sequence is as follows :

0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots.

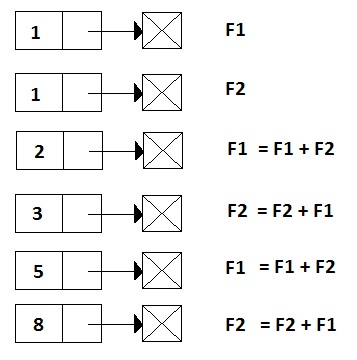
Each successive number is equal to the sum of the two preceding numbers. If you wanted to find the 5th number of the sequence it would be 5.

F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 F11 F12
0 1 1 2 3 5 8 13 21 34 55 89 144

This program is implemented with a double linked list. Each Fibonacci number stored as a sequence of integers inside of a list. For example to calculate the 6th number of the Fibonacci sequence it would start out with f1 and f2 lists that have a single node with 1 inside.

Continue reading